모든 것을 다 챙기려다 보면 복잡해진다... 인생이든, 이론이든,,,
항상 중요한 것만 적당하게 챙기는 것. 그것이 중요하다.
그래서 오늘은 적당히 연결하는 Convolution에 대해서 배워보자...
다소 진지하게 써볼 생각이다 today는
📌 Convolutional Layer
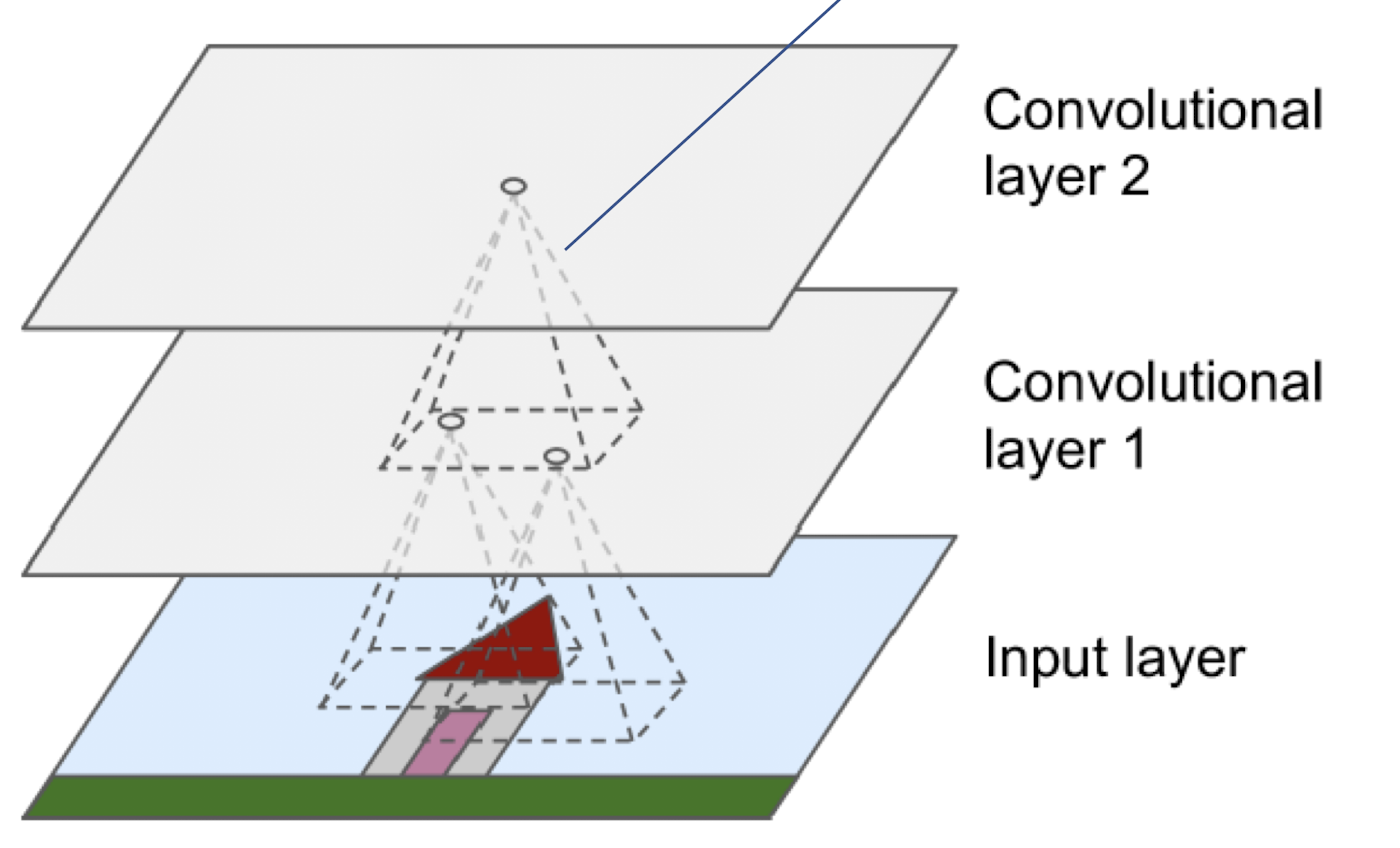
- CNN layer들은 receptive field(수용 영역)이라고 불리는 부분을 통해서 원하는 부분의 정보만 가지고 온다
- input layer에 있는 single pixel들이 모두 연결되는 것이 아니고, receptive field 내의 존재하는 pixel들만 연결된다
- 이것은 계산 복잡도를 줄이는데 아주 효과적인 방법이다
📌 Dense layer VS Convolutional layer


- Dense layer
- input layer에 있는 모든 노드들이 다음 hidden layer에 완전히 연결이 된다
- 모두 연결되어 있다보니 조금만 달라져도 다른 input으로 인식한다(주변의 패턴을 파악할 수 없기에)
- 다른 input으로 인식하게 되면 학습이 이상한 방향으로 진행될 수 있다(ex. 고양이 사진을 조금만 비틀어 input으로 주었는데 고양이라고 인식을 못할 수도 있음)
- Convolutional layer
- kernel 사이즈에 따라서 달라지지만, kernel 내에 존재하는 노드들을 모아서 하나의 노드로 만들기 때문에 주변의 패턴을 파악할 수 있다
- 조그만 변화는 무시될 수 있기에 조금만 달라져도 다른 input으로 인식하는 dense layer의 문제를 해결할 수 있다
- 몇 개의 node를 묶어 하나의 node를 만들기에 hidden layer의 크기는 작아진다
📌 Padding

- convolutional layer를 거치면 크기가 작아지게 되는데 이것을 막기 위해 주변의 0의 값을 가진 pixel을 추가하여 layer를 거치더라도 크기가 작아지지 않도록 하는 것이다
📌 Stride
- kernel이 움직이는 거리.
- stride가 2라면 위 그림에서 빨간색 이후 파란색이 될 때 2칸씩 움직인다는 것을 의미한다
- stride가 커질수록 output의 크기는 줄어든다
📌 Filters

- 보고 싶은 부분만 보고 나머지는 걸러내기 위한 도구라고 생각하면 쉽다
- filters 또는 convolutional kernel이라고 부르기도 한다
- input값에 filter값들을 곱한 후 그것들을 다 더해서 feature map의 값으로 지정한다(weighted sum)
- filter는 activation function처럼 특정 부분을 output으로 넘겨줄 것인가, 안 넘겨줄 것인가의 역할도 한다(ex. horizontal line filter를 사용하면 가로의 특징이 부풀어져있는 feature map이 output으로 나올 것이다)
📌 Stacking Multiple Feature Maps
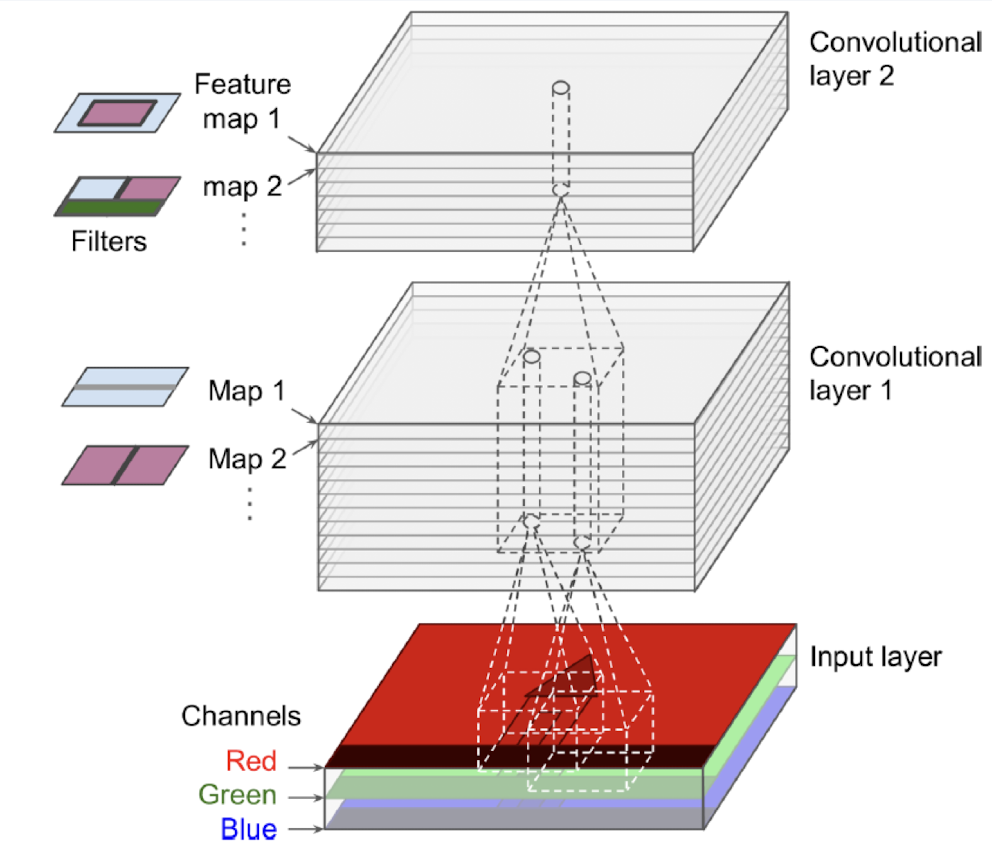
- input에 여러 종류의 trainable filter를 동시에 적용시켜 여러가지 특징들을 찾아낼 수 있도록 할 수 있다
📌 Equation
$$z_{i,j,k}=b_k - \sum^{f_h-1}_{u=0}\sum^{f_w-1}_{v=0}\sum^{f_n'-1}_{k'=0}x_{i',j',k'} \times w_{u,v,k',k} $$
$$ with \ \ \ \ i'=i\times s_h + u ,\ \ \ j'=j\times s_w+v$$

- $z_{i,j,k}$ : 컨볼루션 레이어(layer L)의 feature map k의 i열, j열에 위치한 뉴런의 출력이다.
- $s_h, s_w$ : vertical, horizontal stride
- $f_h, f_w$ : receptive field의 height, width
- $f_{n'}$ : 이전 layer(layer L-1)의 feature map의 수
📌 Code
conv = keras.layers.Conv2D(filters=32, kernel_size=3, strides=1, padding="same", activation="relu")- 사람이 조절할 수 있는 hyperparameter : filter, kernel size, stride, padding
- padding="valid" : padding을 하지 않는 것. 끝부분이 무시될 수도 있음
- padding="same" : padding을 하는 것. 보통 kernel_size-1/2이다
📌 Pooling layer

- to subsample the imput image
- 계산 복잡도, 메모리 사용량 및 hyperparameter 수를 줄이기 위해
- 이것은 overfitting을 막는 해결책이 될 수 있다
- 이전 layer를 연결하는 것은 conv layer와 동일
- weight가 없다. 즉, parameter가 없다
- input에서 max, mean 값을 추출하여 output값을 낸다
- 2x2 pooling kernel, stride=2, no padding -> 크기가 절반이 된다
- 장점
- 작은 이동에는 변하지 않는(invariance) 성질이 있다
- 단점
- loss 되는 것이 많다. (2x2 kernel with stride 2)에서는 75%정도가 loss된다
- detail이 중요한 segmentation과 같은 분야에서는 적절하지 않다
- 해상도가 줄어든 상태로 다음 convolutional layer로 전달하기 때문에 어떤 feature map이 중요한지 쉽게 판단할 수 있다
📌 Dropout
- overfitting을 방지하기 위한 역할이다
- ex. Dropout(0.5) : 노드의 50%만 활성화하여 다음 layer와 연결한다
📌 Flatten()
- input 데이터를 1차원으로 바꿔주는 역할이다
📌 model code
model = keras.models.Sequential([
keras.layers.Conv2D(64, 7, activation="relu", padding="same", input_shape=[28, 28, 1]),
keras.layers.MaxPooling2D(2),
keras.layers.Conv2D(128, 3, activation="relu", padding="same"),
keras.layers.Conv2D(128, 3, activation="relu", padding="same"),
keras.layers.MaxPooling2D(2),
keras.layers.Conv2D(256, 3, activation="relu", padding="same"),
keras.layers.Conv2D(256, 3, activation="relu", padding="same"),
keras.layers.MaxPooling2D(2),
keras.layers.Flatten(),
keras.layers.Dense(128, activation="relu"),
keras.layers.Dropout(0.5),
keras.layers.Dense(64, activation="relu"),
keras.layers.Dropout(0.5),
keras.layers.Dense(10, activation="softmax")
]}- 원래 convolution을 한 번하고, pooling을 한 번해야 하지만 maxpooling으로 해상도를 떨어지게 함으로써 convolution을 2번 진행해도 된다(input의 차원이 낮아 2번 진행해도 계산이 많지 않음)
- dense에 들어가기 전 flatten으로 1차원을 만든다
- dense layer에서 input data는 많은데 적은 개수의 dense layer를 구성하면 적절히 가중치를 설정할 수 없다(너무 쥐어짜면 정보를잃어버릴 가능성이 있다)
- filter는 feature map 이라고 생각해도 된다
📌 parameter 수 계산

- 1st Conv2D : (3x3) x 32 + 32 = 320 [kernel size x input filter x output filter + output bias(filter수랑 동일)]
- 2nd Conv2D : (3x3) x 32 x 64 + 64 = 18496 [kernel size x input filter x output filter + output bias]
- 3rd Conv2D : (3x3) x 64 x 128 + 128 = 73856
- 1st dense : 1152 x 128 + 128 [input size x output size + output bias]
- 2nd dense : 128 x 10 + 10 [input size x output size +output bias]
'학교 공부 > 기계학습개론' 카테고리의 다른 글
| 21. RNN Part II(Code) & Autoencoder (0) | 2022.12.14 |
|---|---|
| 20. RNN (0) | 2022.12.14 |
| 19. Famous CNN architecture - Part 2 (0) | 2022.12.14 |
| 18. Famous CNN Architectures (2) | 2022.12.12 |
| 16. DNN (2) | 2022.11.30 |
