학교 공부/컴퓨터비전
13. Classification & Image Pattern Recognition 1
경북대학교컴퓨터학부
2022. 12. 9. 17:56
한 번만에 어떤 것을 보고, 이것의 정답을 맞출 수 있을까?
우리는 어릴 때 항상 틀리면서 정답을 찾았다.
틀리면서 무엇을 배웠고, 어떻게 하면 정답을 빨리 맞출 수 있는지 그것이 핵심이다.
틀리는 것을 두려워말고, 틀린 것을 기반으로 빨리 맞추려고 해야하지 않을까
📌 Classification
- 한 장의 이미지를 모델에 input으로 주면, 그 이미지가 어떤 label에 속하는지 알려주는 것
- e. g.) 객체 검출, 생체 인식
- model) Bayes Classifier, KNN, Neural Net, SVM, Decision Tree
📌 Pattern Recognition
- Machine Learning -> Pattern Recognition -> Classification
- K-means 알고리즘에서는 데이터를 나누기 위해 패턴을 찾는다
📌 Pattern Recognition Basic Approach
- Structural Approach
- 패턴의 structural feature를 정의하고, 그것을 기반으로 structural similarity를 측정하여 분류한다
- 사람의 표정과 같이 structural feature를 추출하기 어려울 때는 한계가 발생한다
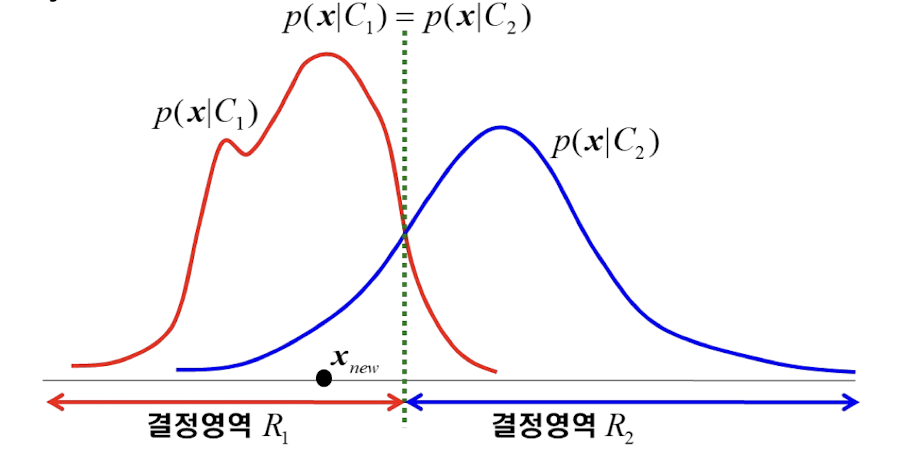
- Statistical Method
- statistical model을 기반으로 분류한다
- 데이터가 들어왔을 때 가장 확률이 높은 label로 분류를 진행한다
- 베이즈의 결정 규칙(사전 정보가 주어지는 경우 사용 가능, 정보가 있어야 확률을 측정할 수 있으므로)에 기반하여 결정한다
- Data driven method
- 데이터로부터 class distribition을 배우고, 그것을 기반으로 분류한다
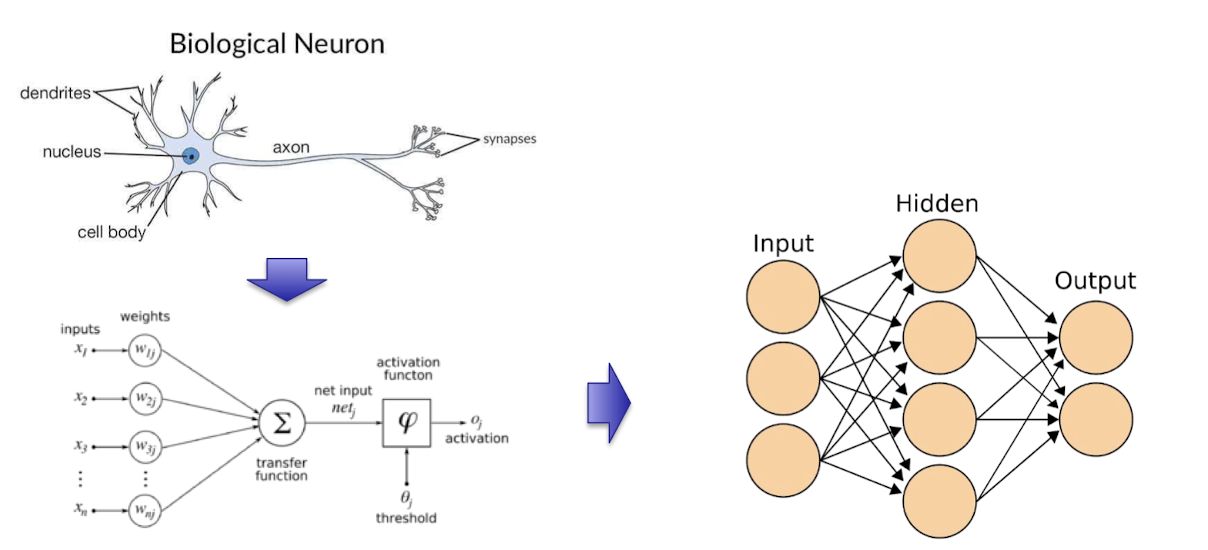
- Neural Network Approach
- 사전 지식이 아닌 학습을 통해 결정 경계를 학습하여 패턴을 인식하여 분류한다
📌 패턴 인식의 어려움
- 노이즈로 인한 이미지 데이터의 다양한 변수
- Artifact(이미지에 필요 없는 것이 촬영되는 경우를 의미한다)
- Unknown Facts
📌 Classifier as a Learning System
- Input : Data set (A set of input-output sample pairs)
- output : Class Label

- $ g(x; \theta) $ : 활성화함수 (label을 결정해주는 함수)
- goal : 분류 오차를 최소화하는 최적의 결정 경계를 찾는 것
- error
- training error : 학습 데이터에 대해 분류 오차를 계산한 것
- test error : 실제 데이터에 대해 분류 오차를 계산한 것
📌 Estimation of Generalization Error
- 일반화 오차 : test sample이 제한적일 때, 확률분포함수를 이용한 분포에 따른 "평균" 오차값. 테스트 오차가 왜곡을 가질 수 있으므로
- Cross Validation Method
- 일반적으로 training set으로 모델을 훈련시키고, test set으로 모델을 검증한다. 하지만 고정된 test set을 통해 모델의 성능을 검증하다보면, 모델은 test set에만 overfitting되게 된다. 이를 방지하기 위해 교차 검증을 한다.
- training set을 training set + validation set으로 분리한 뒤, validation set을 사용해 검증하는 방식이다
- K-fold cross validation
- 알고리즘
- 전체 데이터 셋을 Training Set과 Test Set으로 나누다.
- Training Set 을 Training Set + Validation Set으로 사용하기 위해 k개의 fold로 나눈다.
- Fold 1을 Validation Set으로 사용하고 나머지 fold를 Training Set으로 사용한다.
- 모델을 Training 한 뒤, Validataion Set (Fold 1)으로 평가한다.
- 차례대로 다음 Fold를 Validation Set으로 사용하며, 3번을 반복한다.
- 총 k개의 성능 결과가 나오며, 이 k개의 평균을 해당 학습 모델의 성능이라고 한다.
- 알고리즘

📌 Approaches of Obtain Decision Boundary
- Discriminative Method (판별 방법)
- 판별 함수를 만들어 활용하는 방식이다.
- 판별 함수란, 각각의 벡터 X를 특정 클래스에 바로 배정하는 함수이다.
- ex) 선형 분류기, 퍼셉트론, SVM
- Generative Method (생성적 방법)
- 결정 규칙을 찾기 위하여 각 클래스의 분포를 이용하여 추정한다.
- 조건부확률 밀도 분포와, 클래스의 확률 밀도 분포를 모델링한 후, 베이지안 정리를 이용하여 계산하는 방식이다.
- Distance Based Method
- 클래스의 멤버를 데이터 간의 거리에 기초하여 결정하는 방법이다.
- ex) K-Nearest Neighbor Classifier
- K-NN 알고리즘의 설명
- 아래 그림에서 빨간색 세모는 어느 그룹에 속한다고 할 수 있을까?
- K-NN 알고리즘에 따르면, K는 내 주변의 거리가 가까운 K개의 데이터를 확인해보겠다는 의미이다. K=1일 경우에는 초록색 그룹으로 분류될 수 있고, K=3일 경우에는 노란색 그룹으로 분류될 수 있다. 항상 분류가 가능하도록 K는 홀수로 설정하는 것이 좋다

📌 Linear Decision Function
- $ g_i(x)=w_i^Tx+w_{i0}=\sum^n_{j=1}w_{ij}x_j+w_{i0}$
- input : N-dimensional input $x=[x_1, x_2, ... , x_n]^T
- $w_i$ : i번째 weight
- $w_{i0} : bias weight
📌 Polynomial Decision Function
- $g_i(x)=x^TW^ix+w_i^Tx+w_{i0}$
- input : $n^2+n+1
- p-th order polynomial : $O(n^p)$
📌 Linear decision function의 한계
- 아래의 그림에서 초록색 부분은 linear function으로 결정할 수 없다
- Decision rule로 극복할 수 있다


- 최적화할 수 있는 파라미터를 찾는 것이 핵심. 즉, $J(w_i)$를 최소화하는 것이 핵심
📌 Perceptron as a Linear Classifier
- random 값으로 weight parameter를 초기화한다
- 주어진 input에 대해서 output을 계산한다
- output과 기존의 label 사이의 차이를 계산한다
- 차이를 기반으로 weight parameter를 조정한다
- 계속 반복
